Recently, Associate Professor Baoheng Yao’s research team from the School of Oceanography at Shanghai Jiao Tong University published a study titled **"A novel flexible fixed-time stability result and its application in sliding-mode controller design"** in the authoritative journal Nonlinear Dynamics, a leading publication in nonlinear dynamics and control. Collaborators include Shanghai Jiao Tong University doctoral candidates Yu Cao, Hao Wen, and Xu Zhang, postdoctoral researcher Hexiong Zhou, and Professor Lian Lian. The School of Oceanography at Shanghai Jiao Tong University is the primary affiliation, with Associate Professor Baoheng Yao serving as the corresponding author.

Fixed-time stability theory, a critical branch of modern control theory, ensures that system states converge  to equilibrium within a fixed time independent of initial conditions by adjusting system dynamics into specific forms. This property holds significant value for engineering applications such as robotic control. However, traditional methods struggle to balance convergence speed with convergence time estimation accuracy, while also facing challenges in parameter tuning. Although existing studies propose parameter adjustment strategies for fixed-time stable systems, current theories suffer from unclear mechanistic roles of parameters and overly complex system formulations. Addressing these limitations, Associate Professor Yao’s team leveraged Lyapunov theory to develop a hyperbolic cosine-power function hybrid fixed-time stability theory, simplifying system structures while clarifying parameter roles. Based on this theory, they further proposed a sliding-mode control method for second-order uncertain systems, laying a theoretical foundation for motion control in marine robotics and related engineering applications.

1.Parameter Simplification: Reduced the number of parameters affecting convergence time from five to three, with clearly defined functional roles for each parameter. This significantly lowers design complexity without compromising system tunability;

2.Performance Tunability: Analyzed the mechanistic impact of parameters on convergence dynamics, including convergence time, rate, chattering suppression, and initial control input. Provided guidelines for parameter adjustment to enable flexible switching between control modes;

3.Control Methodology: Derived a sliding-mode control framework for second-order uncertain systems, combining the advantages of the proposed theory with sliding-mode control. This advances practical applications in marine engineering;

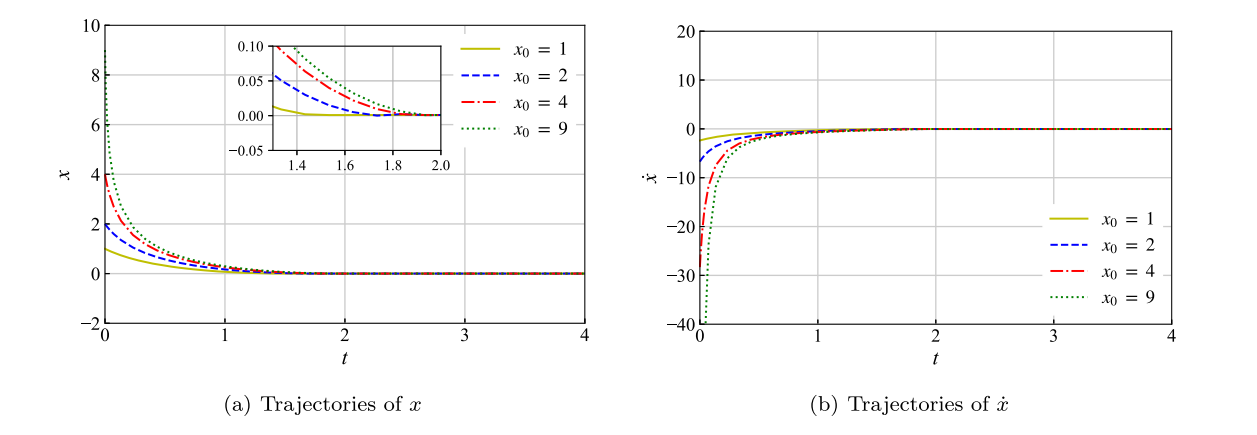
                                           Figure 1: Validation of fixed-time stability in the system.

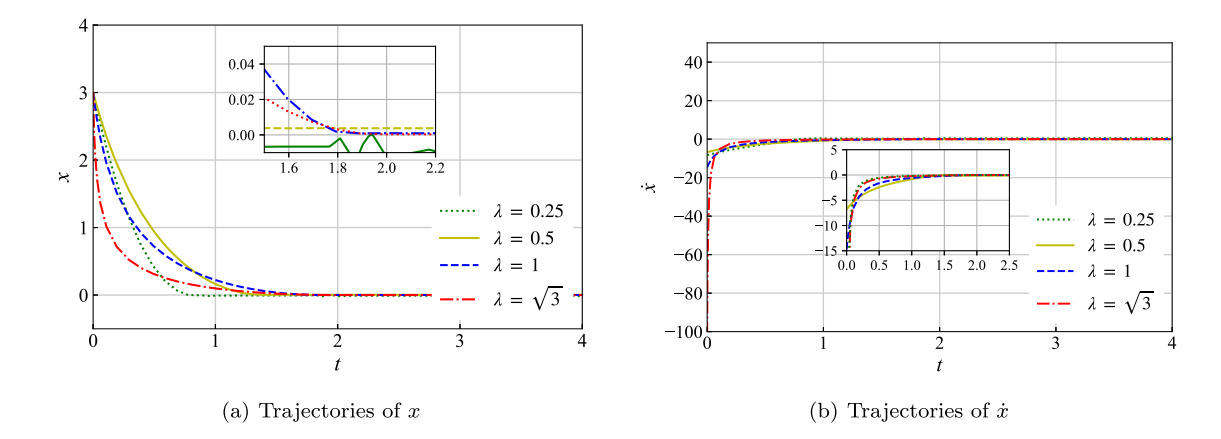
                      Figure 2: Impact of parameter adjustments on system convergence performance.

The research team validated the effectiveness of the proposed theory through numerical simulations. The numerical simulation results demonstrated that the stability theory ensures fixed-time convergence performance of the system (Figure 1). Furthermore, when parameters were adjusted, the system performance followed the trends analyzed in the paper (Figure 2), highlighting the method's flexibility and practical application potential. Subsequently, the team will utilize this stability theory alongside the unmanned surface vehicle (USV) algorithm validation platform developed by doctoral candidate Hao Wen (Figure 3) to verify the algorithm's effectiveness and superiority in marine robotic motion control, thereby enhancing the controllability and safety of oceanographic equipment. 

                  Figure 3: Unmanned surface vehicle (USV) algorithm validation platform.

This study was supported by the National Key R&D Program of China (2021YFC2801600) and other funding sources.

Paper link: https://doi.org/10.1007/s11071-025-11035-0